心理学と勉強法 第19回 考える(推論)
- 2021.07.4 | 心理学と勉強法 高校生・受験生の学び(現在)
第19回は、考える(推論)について説明します、
(2)考える(推論)
知っている知識(既有知識)だけでは、新しい世界が広がりません。人間は考える葦です。持っている知識を活用して新しい知識を獲得するために考えます。考えるときに、ある事を前提として何らかの結論を得ることを推論と呼びます。帰納法や演繹法は、推論の分類です。推して測り、自分(心)を諭す。ということでしょうか。
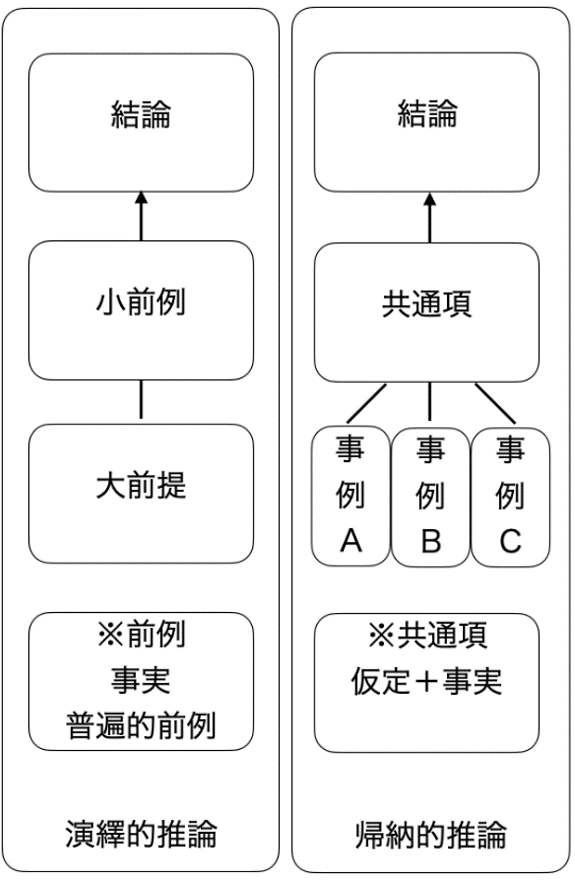
1. 帰納的推論と演繹的推論
帰納的推論とは、いくつかのことから一般的にこうだろうと考えるような推論の仕方です。イギリスの哲学者フランシス=ベーコン(英、1561~1626)が唱え、ロック(英、17世紀)やヒューム(英、18世紀)により発展した哲学(経験論)と言われています。
帰納法的な科学的推論として、ニュートンの万有引力が逸話としてよく挙げられます。万有引力の発見はりんごが木から落ちるのを見て、全てのものには重力があるのかもしれない、と帰納的な推論をニュートンがしたことがきっかけとなったという逸話です。

ただ、帰納的推論で気をつけなければいけないことは、事例からの推論なので、そこに共通点があったとしても推論の結論が必ずしもすべてに当てはまる正しい推論とは限らないことです。
演繹的推論とは、あることが正しいことを前提にして、その前提からきっとこうだろうと考えるような思考のことです。演繹法の一つとして三段論法が有名です。
”すべての人は死ぬ。ソクラテスは人だ。だから、ソクラテスは死ぬ。”という論法です。(三段論法はアリストテレスが唱えた論理学で言及されています。)
数学の定理を使って結論を導くというのも演繹的な推論です。「三角形の内角の和は180度である」という定理を元に、ある三角形の2つの内角の和が120度ということがわかれば、残りの内角は60度だと考えられる、と言ったような推論の方法です。
大学の入学試験では、多くの場合、公式や定義の知識を元に個々の具体的な問題に当てはめることができるかどうかが試される問題が出題されますので、演繹的な推論を試されている場合が多いですね。
数学Ⅰで学ぶ「命題と条件」を思い出してください。逆や対偶という言葉を覚えていますか?推論する上での一つの道筋を示しています。